Announcing: "hashtables", a new Haskell library for fast mutable hash tables
I’m very pleased to announce today the release of the first version of hashtables, a Haskell library for fast mutable hash tables. The hashtables library contains three different mutable hash table implementations in the ST monad, as well as a type class abstracting out the functions common to each and a set of wrapper functions to use the hash tables in the IO monad.
What’s included?
The hashtables library contains implementations of the following data structures:
Data.HashTable.ST.Basic: a basic open addressing hash table using linear probing as the collision resolution strategy. On a pure speed basis, this should be the fastest currently-available Haskell hash table implementation for lookups, although it has a higher memory overhead than the other tables. Like many hash table implementations, it can also suffer from long delays when the table is grown due to the rehashing of all of the elements in the table.Data.HashTable.ST.Cuckoo: an implementation of Cuckoo hashing, as introduced by Pagh and Rodler in 2001. Cuckoo hashing features worst-case O(1) lookups and can reach a high “load factor”, meaning that the table can perform acceptably well even when more than 90% full. Randomized testing shows this implementation of cuckoo hashing to be slightly faster on insert and slightly slower on lookup thanData.HashTable.ST.Basic, while being more space-efficient by about a half word per key-value mapping. Cuckoo hashing, like open-addressing hash tables, can suffer from long delays when the table is forced to grow.Data.HashTable.ST.Linear: a linear hash table, which trades some insert and lookup performance for higher space efficiency and much shorter delays during table expansion. In most cases, randomized testing shows this table to be slightly faster thanData.HashTablefrom the Haskell base library.
Why Data.HashTable is slow
People often remark that the hash table implementation from the Haskell base library is slow. Historically, there have been a couple of reasons why: firstly, Haskell people tend to prefer persistent data structures to ephemeral ones. Secondly, until GHC 6.12.2, GHC had unacceptably large overhead when using mutable arrays due to a lack of card marking in the garbage collector.
However, performance testing on newer versions of GHC still shows the hash table implementation from the Haskell base library to be slower than it ought to be. To explain why, let’s examine the data type definition for Data.HashTable:
data HashTable key val = HashTable {
cmp :: !(key -> key -> Bool),
hash_fn :: !(key -> Int32),
tab :: !(IORef (HT key val))
}
data HT key val
= HT {
kcount :: !Int32, -- Total number of keys.
bmask :: !Int32,
buckets :: !(HTArray [(key,val)])
}For now, let’s ignore the HashTable type, as it is essentially just an IORef wrapper around the HT type, which contains the actual table. The hash table from Data.HashTable uses separate chaining, in which keys are hashed to buckets, each of which contains a linked list of (key,value) tuples. To explain why this is not an especially smart strategy for hash tables in Haskell, let’s examine what the memory layout of this data structure looks like at runtime.
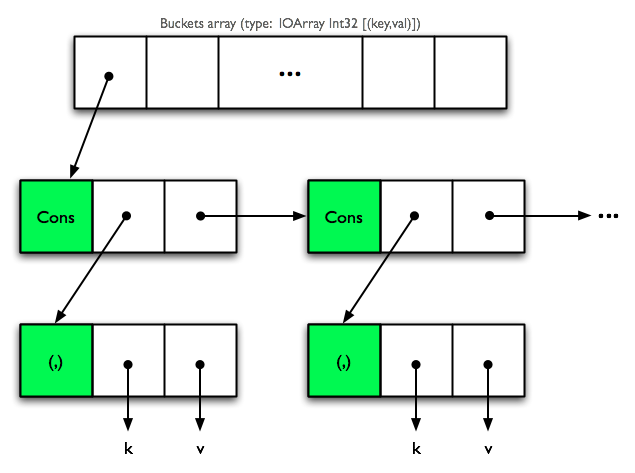
Memory layout of Data.HashTable
Each arrow in the above diagram represents a pointer which, when dereferenced, can (and probably does) cause a CPU cache miss. During lookup, each time we test an entry in one of the buckets against the lookup key, we cause three cache lines to be loaded:
- one for the cons cell itself
- one for the tuple
- one for the key
If the average bucket has b elements in it, the average successful lookup causes 1 + 3b/2 cache line loads: one to dereference the buckets array to get the pointer to the first cons cell, and 3b/2 to find the matching key in the buckets array. An unsuccessful lookup is worse, causing a full 1 + 3b cache line loads, because we need to examine every key in the bucket.
Why this new library is faster
The datatype inside Data.HashTable.ST.Basic looks like this:
data HashTable_ s k v = HashTable
{ _size :: {-# UNPACK #-} !Int
, _load :: !(U.IntArray s)
, _hashes :: !(U.IntArray s)
, _keys :: {-# UNPACK #-} !(MutableArray s k)
, _values :: {-# UNPACK #-} !(MutableArray s v)
}Here, to avoid pointer indirections, I’ve flattened the keys and values into parallel arrays, and stored the hash code for every cell in an unboxed array to speed lookups. Lookup in these three parallel arrays looks like this:
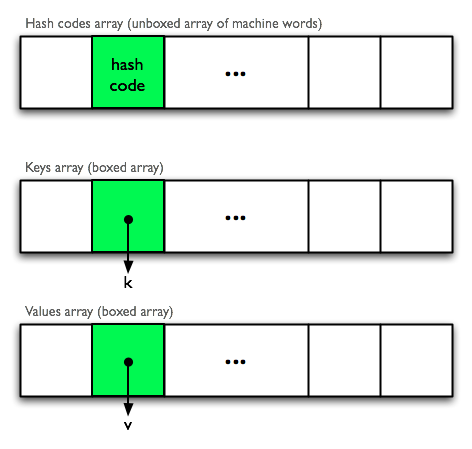
Memory layout of Data.HashTable.ST.Basic
The coloured region represents the location of the key we are looking for. Counting the cache line loads for a typical successful lookup in this structure:
- one, maybe two, to find the correct hash code in the hash codes array. Note that since this is a contiguous unboxed integer array, a cache line load causes eight (sixteen on 32-bit machines) hash codes to be loaded into cache at once.
- one to dereference the key pointer in the keys array.
- one to dereference the key.
- one to dereference the value pointer in the values array.
Unsuccessful lookups are even faster here, since we don’t touch the keys or values arrays except on hash collisions. Astute readers will wonder why we store the hash codes in the table, because this isn’t always done. There are a couple of reasons:
- we can use the hash code slot to mark the cell as empty or deleted by writing a privileged value (zero or one). If we didn’t do this, we would either have to use a datatype something like
Maybein the keys array to distinguish empty or deleted entries, causing an extra indirection, or we would have to play tricks withunsafeCoerceand/orreallyUnsafePtrEquality#(the linear hash table actually uses these tricks to save indirections, but they’re marked “unsafe” for a reason!) - For the types we really care about (specifically
ByteString,Text, andSmallString), theEqinstance is O(n) in the size of the key, as compared to the O(1) machine instruction required to compare two hash codes. - Keeping the hash codes in an unboxed array allows us to do super-efficient branchless cache line lookups in C. Moreover, we can take advantage of 128-bit SSE4.1 instructions on processors which support them (Intel chips, Core 2 and above) to make searching cache lines for hash codes even faster.
- I tested it both ways, and storing the hash codes was consistently faster.
Performance measurements
I ran benchmarks for lookup and insert performance of the three hash table implementations included in the hashtables library against:
Data.HashTablefrom the base libraryData.Mapfrom the base libraryData.HashMap.Strictfrom the unordered-containers library
Unfortunately I cannot release the benchmark code at this time, as it relies on an unfinished data-structure benchmarking library based on criterion, for which I have not yet sought permission to open-source.
The methodology for lookups is:
- create a vector of
Nrandom key-value pairs, where the key is a randomByteStringconsisting of ASCII hexadecimal characters, between 8 and 32 bytes long, and the value is anInt - load all of the key-value pairs into the given datastructure
- create a vector of
N/2random successful lookups out of the original set - perform all of the lookups, and divide the total time taken by the number of lookups to get a per-operation timing
- repeat the above procedure using criterion enough times to be statistically confident about the timings
The above procedure is repeated for a doubling set of values of N from 250 through to 2,048,000. Note that, to be fair and to ensure that random fluctuations in the input distribution don’t influence the timings for the different data structures, each trial uses the same input set for each data structure. We also force a garbage collection run between trials to try to isolate the unpredictable impact of garbage collection runs as much as possible.
The methodology for inserts is similar:
- create a vector of
Nrandom key-value pairs as described above - time how long it takes to load the
Nkey-value pairs into the given data structure. Where applicable, the data structure is pre-sized to fit the data set (i.e. for the hash tables). Note here, though, that I’m not being 100% fair toData.HashTablein this test, as thenewHintfunction wasn’t called — when I tried to use it, the benchmark took forever. I’m ashamed to say that I didn’t dig too deeply into why.
The benchmarks were run on a MacBook Pro running Snow Leopard with an Intel Core i5 processor, running GHC 7.0.3 in 64-bit mode. The RTS options passed into the benchmark function were +RTS -N -A4M.
Lookup performance
| Avg time per lookup (seconds) | |
| Input Size |
Lookup performance, log-log plot
| Avg time per lookup (seconds) | |
| Input Size |
Insert performance
| Avg time per insert (seconds) | |
| Input Size |
Insert performance, log-log plot
| Avg time per insert (seconds) | |
| Input Size |
Performance measurements, round 2
My first thought upon seeing these graphs was: “what’s with the asymptotic behaviour?” I had expected lookups and inserts for most of the hash tables to be close to flat, especially for cuckoo hash, which is guaranteed O(1) for lookups in the worst case. I had some suspicions, and re-running the tests with the RTS flags set to +RTS -N -A4M -H1G (specifying a 1GB suggested heap size) seems to confirm them:
Lookup performance
| Avg time per lookup (seconds) | |
| Input Size |
Lookup performance, Log-log plot
| Avg time per lookup (seconds) | |
| Input Size |
Insert performance
| Avg time per insert (seconds) | |
| Input Size |
Insert Performance, Log-log plot
| Avg time per insert (seconds) | |
| Input Size |
These are more or less the graphs I had been expecting to see. The main impact of setting -H1G is to reduce the frequency of major garbage collections, and the difference here would suggest that garbage collection overhead is what’s causing the poorer-than-expected asymptotic performance. The linear probing and cuckoo hash tables included in this library use very large boxed mutable arrays. The GHC garbage collector uses a card marking strategy in which mutable arrays carry a “card table” containing one byte per k entries in the array (I think here k is 128). When the array is written to, the corresponding entry in the card table is marked “dirty” by writing a “1” into it. It would seem that the card table is scanned during garbage collection no matter whether the array has been dirtied or not; this would account for the small linear factor in the asymptotic time complexity that we’re seeing here.
Conclusion
While Haskell people prefer to use immutable/persistent data structures in their programs most of the time, there are definitely instances in which you want a mutable hash table: no immutable data structure that I know of supports O(1) inserts and lookups, nor is there an immutable data structure that I know of which can match a good mutable hash table for space efficiency. These factors are very important in some problem domains, especially for things like machine learning on very large data sets.
The lack of a really good Haskell hash table implementation has been a sticking point for quite some time for people who want to work in these problem domains. While the situation is still not as good as it might eventually be due to continuing concerns about how the GHC garbage collector deals with mutable arrays, it’s my hope that the release of the hashtables library will go a long way towards closing the gap.
The source repository for the hashtables library can be found on github. Although I’ve made substantial efforts to test this code prior to release, it is a “version 1.0”. Please send bug reports to the hashtables github issues page.
Update (Oct 21, 2011)
A fellow by the name of Albert Ward has translated this blog post into Bulgarian.
Comments
blog comments powered by Disqus